El tamaño del efecto de Cohen
Supongamos que un investigador pretende comprobar la efectividad de un tratamiento para la depresión. Para ello, selecciona una muestra de 200 personas con el mismo grado y tipo de depresión, y asigna aleatoriamente a 100 de esas personas al grupo experimental y a las 100 restantes al grupo control. A continuación, administra el tratamiento únicamente a los miembros del grupo experimental. Tras la intervención, aplica un test para medir el bienestar de los participantes y obtiene las siguientes medias:
- Grupo control: 30 puntos
- Grupo experimental: 33 puntos
Estos resultados parecen apoyar la efectividad de su tratamiento, pero, para estar seguro de sus resultados realiza un contraste de hipótesis para comprobar si esa diferencia de medias es estadísticamente significativa o es atribuible a los efectos del azar. Tras los cálculos correspondientes, nuestro protagonista observa que las diferencias entre el grupo experimental y el grupo control son significativas, concluyendo que la intervención es efectiva para el tratamiento de la depresión.
Sin embargo, un compañero de laboratorio le hace darse cuenta de lo precipitado de su conclusión: “has encontrado diferencias significativas entre ambos grupos, pero no conoces la relevancia de esas diferencias”, y finaliza la conversación recomendándole complementar sus análisis con el cálculo del tamaño del efecto.
El tamaño del efecto es el nombre asignado a una familia de índices cuyo objetivo es medir la magnitud del efecto estudiado, en nuestro ejemplo, la magnitud (estandarizada) de la diferencia entre la media del grupo control y la del grupo experimental. En el caso de los contrastes de diferencia de medias, uno de los índices más empleados es la d de Cohen.
Imaginemos que nuestro investigador calcula la d de Cohen de su contraste y obtiene 0,30… ¿qué implicaciones prácticas tiene este resultado? Para ilustrarlo vamos a representar gráficamente, a través de dos histogramas, las puntuaciones del grupo control (azul oscuro) y las del grupo experimental (azul claro):
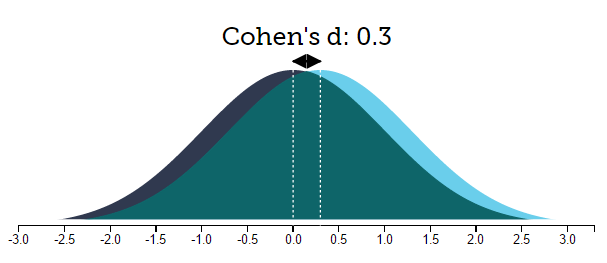
Como se puede observar, las medias, y las distribuciones de las puntuaciones, se encuentran realmente muy cercanas, hasta tal punto que el porcentaje de solapamiento entre las puntuaciones de ambos grupos es del 88%. De hecho, tan sólo el 58% de las personas del grupo experimental tendrán una puntuación de bienestar superior a la media del grupo control. Teniendo en cuenta estos resultados, es probable que nuestro investigador reconsiderase la efectividad de su tratamiento.
Imaginemos ahora que, en base a la ineficacia de su anterior tratamiento, nuestro investigador decide no tirar la toalla y desarrolla un nuevo tratamiento contra la depresión. Tras un diseño experimental similar al anterior, y obtener de nuevo diferencias significativas entre los grupos, encuentra una d de Cohen de 1,5:
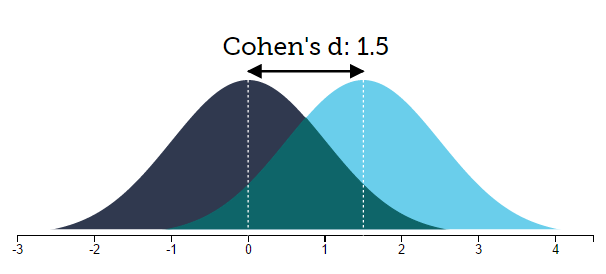
En esta ocasión, parece que los resultados han sido mejores. El porcentaje de solapamiento entre las puntuaciones de ambos grupos ha descendido hasta el 43%. Por otro lado, el 93% de las personas del grupo experimental tendrán una puntuación de bienestar superior a la media del grupo control. Nuestro investigador puede, finalmente, asegurar que su nuevo tratamiento es eficaz ante la depresión.
Como conclusión diremos que la prueba de significación no es intrínsecamente negativa, de hecho, cumple una función importante y necesaria en el ámbito de la investigación. Lo problemático es interpretar esta prueba de forma inadecuada y sin acompañarla del tamaño del efecto, lo que nos puede llevar a establecer conclusiones erróneas.
¿Estás buscando al candidato ideal para tu empresa pero no sabes por dónde empezar? En Facthum podemos ayudarte con nuestra sección de Assessment, donde contamos con un equipo de evaluación experimentado que te guiará en tus procesos de evaluación para encontrar al candidato perfecto.
Nuestro equipo de evaluación está altamente capacitado y cuenta con una amplia experiencia en la realización de diferentes pruebas de evaluación que permiten medir el desempeño y las habilidades de los candidatos en áreas específicas. Además, nuestra metodología de evaluación está diseñada para identificar las fortalezas y áreas de mejora de cada candidato, lo que nos permite ofrecerte una evaluación integral y detallada.
En Facthum, creemos que la evaluación es una herramienta esencial para la selección de personal y para garantizar el éxito de cualquier empresa. Por ello, trabajamos de la mano de nuestros clientes para entender sus necesidades y ofrecerles soluciones personalizadas como T3 Assessment que se adapten a sus requerimientos específicos.
No pierdas más tiempo en procesos de selección que no te dan los resultados que necesitas. Confía en nuestro equipo de evaluación de Facthum y consigue al candidato que estás buscando. ¡Contáctanos y descubre cómo podemos ayudarte hoy mismo!





